数学,一门知识的连贯性和逻辑性极强的学科,只有理解和掌握数学的概念、法则、公式、定理,把握他们之间的内在联系才能为日后学习打下良好的基础。只有基础扎实,解决问题才能得心应手,成绩才会提高。要深入了解一个知识点中的全部内容,下面通过一张坚果云思维导图让你轻松学习函数,掌握函数重点内容。
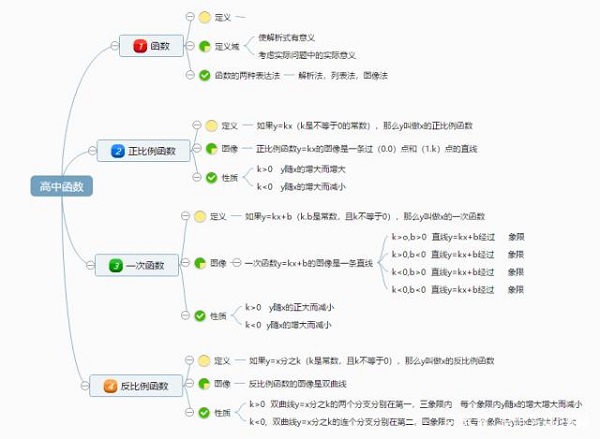
在一个变化过程中,假如有两个变量x,y,如果对任意一个x都有唯一的一个y值和他它对应,那么就称x是自变量,y是x的函数。X的取值范围叫做函数的定义域,y的取值范围叫做函数的值域。
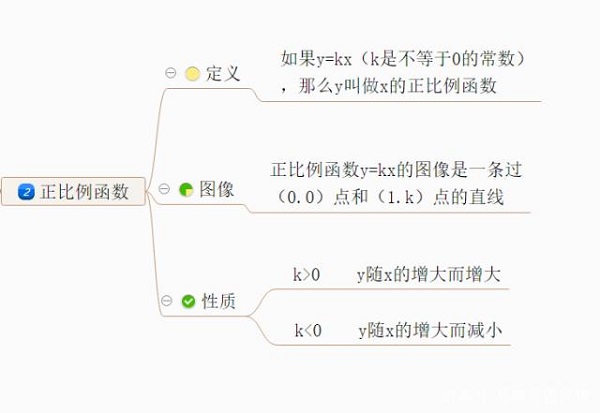
一般地两个变量x,y之间的关系式可以表示成形如y=kx的函数(k为常数,x的次数为1,且k≠0),那么y=kx就叫做正比例函数。
性质:
当k>0时,图像经过第一、三象限,从左往右上升,y随x的增大而增大(单调递增),为增函数;
当k<0时,图像经过第二、四象限,从左往右下降,y随x的增大而减小(单调递减),为减函数。
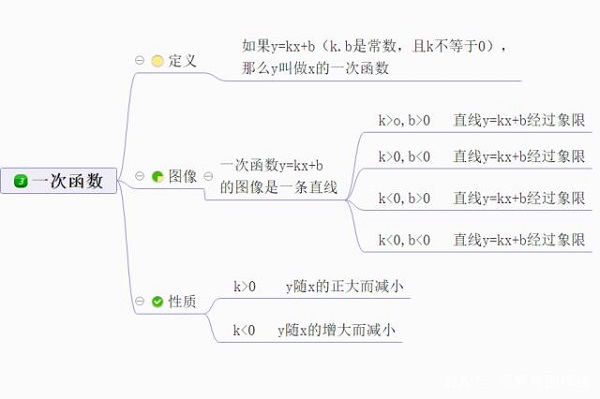
一次函数是函数中的一种,一般形如y=kx+b(k,b是常数,k≠0),其中x是自变量,y是因变量。当b=0时,y=kx+b(k为常数,k≠0),y叫做x得正比例函数
性质:
当k>0时,直线必通过一、三象限,y随x的增大而增大;
当k<0时,直线必通过二、四象限,y随x的增大而减小。
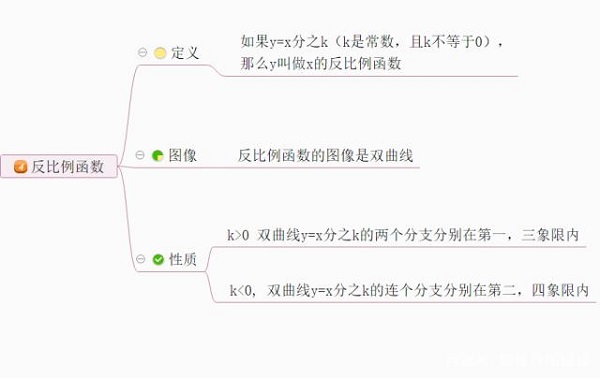
一般地,如果两个变量x、y之间的关系可以表示成y=k/x (k为常数,k≠0)的形式,那么称y是x的反比例函数。
性质
当k>0时,图像分别位于第一、三象限,每一个象限内,从左往右,y随x的增大而减小;
当k<0时,图像分别位于第二、四象限,每一个象限内,从左往右,y随x的增大而增大。
 坚果芸
坚果芸

