иҜҙй«ҳж•°зҡ„иҜқпјҢеҫҲеӨҡдәәдјҡеҫҲдјӨи„‘зӯӢзҡ„гҖӮдҪҶжҳҜиҝҷд№ҹжҳҜжҲ‘们еә”иҜҘйҮҚи§Ҷзҡ„йўҶеҹҹгҖӮй«ҳж•°еңЁжӯӨеҗҺпјҢз ”з©¶з”ҹиҖғиҜ•жҲ–иҖғиҜ•зј–еҲ¶зӯүиҖғиҜ•дёӯпјҢйғҪдјҡиҖғеҲ°вҖӢгҖӮд»Һй«ҳж•°дё»иҰҒеҲҶдёәе…ӯдёӘйғЁеҲҶгҖӮе…¶дёӯжңҖйҮҚиҰҒзҡ„жҳҜдёҚе®ҡз§ҜеҲҶе’Ңе®ҡз§ҜеҲҶгҖӮ他们主иҰҒеҮәзҺ°еңЁи®Ўз®—еӨ§йўҳдёӯеҮәзҺ°пјҢе…¶ж¬ЎжҳҜеҜјж•°пјҢеҫ®еҲҶпјҢжұӮжһҒйҷҗгҖӮжүҖд»ҘеӯҰз”ҹеңЁеӯҰд№ иҝҷйғЁеҲҶзҡ„ж—¶еҖҷиҰҒж јеӨ–еҠӘеҠӣгҖӮдёӢйқўе’Ңе°Ҹзј–дёҖиө·пјҢз”Ёеқҡжһңдә‘жҖқз»ҙеҜјеӣҫиҜҙжҳҺй«ҳж•°зҡ„дё»иҰҒеҶ…е®№пјҢжңҹеҫ…дјҡжңүеё®еҠ©гҖӮ
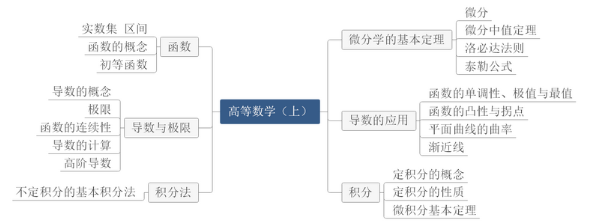
й«ҳж•°жҖқз»ҙеҜјеӣҫ
дёҖпјҡеҮҪж•°
иҝҷйғЁеҲҶеңЁжҲ‘们й«ҳдёӯжҺҘи§ҰиҝҮпјҢеә”иҜҘдёҚйҡҫеӯҰгҖӮеҹәжң¬еҮҪж•°еҒҮи®ҫжңүжӣҙеӨҡзҡ„еҖ’дёүи§’еҪўеҮҪж•°пјҢжүҖд»ҘйңҖиҰҒи®°дҪҸжҜҸдёӘеҖ’дёүи§’еҪўеҮҪж•°зҡ„еҹҹе’ҢеҖјеҹҹгҖӮдҫӢеҰӮпјҢsinxзҡ„еҹҹжҳҜarcsinxзҡ„еҹҹпјҢsinxзҡ„еҹҹжҳҜarcsinxзҡ„еҹҹгҖӮжҢҮе®ҡy(дҫӢеҰӮX y=0)дёҚжҳҜеҚ•зӢ¬еӯҳеңЁзҡ„еҮҪж•°зҡ„ж–°еҗҚз§°вҖ”вҖ”йҡҗејҸеҮҪж•°гҖӮеҲҶзұ»дёәеҹәжң¬д»ҘеӨ–зҡ„еҮҪж•°зұ»гҖӮжҺҘдёӢжқҘпјҢжҲ‘们е°ҶйҖҡиҝҮжҖқз»ҙеҜјеӣҫжқҘдәҶи§ЈиҝҷйғЁеҲҶзҡ„е…¶д»–еҶ…е®№гҖӮ
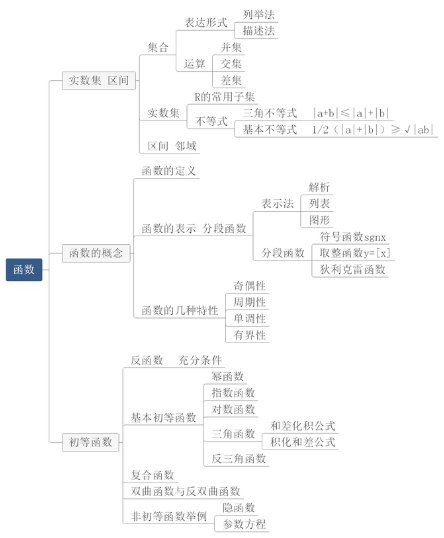
й«ҳж•°жҖқз»ҙеҜјеӣҫ
дәҢпјҡеҜјж•°е’ҢжһҒйҷҗ
еҜјж•°жҲ‘们й«ҳдёӯд№ҹжҺҘи§ҰиҝҮгҖӮеңЁиҝҷдёҖйғЁеҲҶдёӯпјҢжҲ‘们иҰҒйҮҚзӮ№жҠҠжҸЎеҲ©з”Ёеӣӣз§Қиҝҗз®—жүҫеҮәжһҒйҷҗзҡ„ж–№жі•пјҢд»ҘеҸҠиҜұеҜје’Ңиҝһз»ӯд№Ӣй—ҙзҡ„е…ізі»(дёҚдёҖе®ҡжҳҜиҝһз»ӯзҡ„пјҢдҪҶдёҚиҝһз»ӯзҡ„)гҖӮзӯүд»·жҖ§еғҸж— йҷҗзҡ„д»Јжӣҝе…¬ејҸдёҖж ·пјҢеӯҰз”ҹ们дёҖе®ҡиҰҒзүўи®°пјҢеңЁйўҳзӣ®дёӯдёҖе®ҡиҰҒжіЁж„Ҹx0дҪҝз”ЁгҖӮиҝҷйҮҢз»ҷеҗҢеӯҰ们еҲ—дёҫдәҶдёҖдәӣзӯүд»·зҡ„жһҒе°‘ж•°е…¬ејҸгҖӮx вҖ”вҖ” sinx вҖ”вҖ” tanx вҖ”вҖ” arcsinx вҖ”вҖ” arctanxгҖҒx вҖ”вҖ” ln (1 x) вҖ”вҖ”e 2-1зӯүгҖӮ

й«ҳж•°жҖқз»ҙеҜјеӣҫ
дёүпјҡз§ҜеҲҶжі•
з§ҜеҲҶжі•жҳҜйҮҚзӮ№еҶ…е®№пјҢжңүдёӨз§ҚжұӮз§ҜеҲҶзҡ„ж–№жі•пјҢдёҖйҳ¶дәӨжҚўз§ҜеҲҶжі•д№ҹз§°дёәзұійӮЈжүҳеҫ®еҲҶжі•е’ҢдәҢйҳ¶дәӨжҚўз§ҜеҲҶжі•гҖӮеҰӮжһңеңЁжұӮи§Јй—®йўҳж—¶жүҫдёҚеҲ°е…ідәҺдёүи§’еҮҪж•°зҡ„з»ғд№ йўҳпјҢйҖҡеёёдҪҝз”Ёдёүи§’жҒ’зӯүејҸз®ҖеҢ–и§ЈеҶіж–№жЎҲпјҢ然еҗҺиҝӣиЎҢиҮӘеҸҳйҮҸгҖӮйҒҮеҲ°еёҰж №еҸ·зҡ„з§ҜеҲҶжҹҘжүҫзҡ„з»ғд№ пјҢйҰ–е…ҲиҰҒиҖғиҷ‘第дәҢзұ»дә‘з§ҜеҲҶж–№жі•гҖӮ
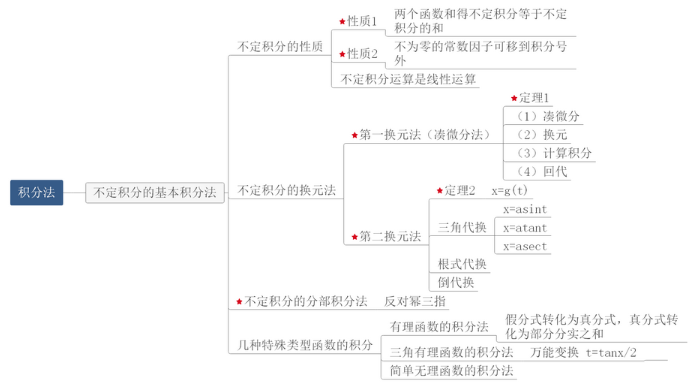
й«ҳж•°жҖқз»ҙеҜјеӣҫ
еӣӣпјҡеҫ®еҲҶзҗҶи®әзҡ„еҹәжң¬е®ҡзҗҶ
еңЁиҝҷйғЁеҲҶдёӯпјҢз»Ҹеёёе°ҶеҜ№жӢүж јжң—ж—ҘдёӯеҖје®ҡзҗҶзҡ„зҗҶи§ЈдҪңдёәиҜҒжҳҺй—®йўҳиҝӣиЎҢжҺўи®ЁпјҢеңЁеҒҡиҜҒжҳҺй—®йўҳж—¶жіЁж„ҸеҸҳеҪўпјҢжҺҘиҝ‘жӢүж јжң—ж—ҘдёӯеҖје®ҡзҗҶе…¬ејҸгҖӮд»Ҙf(x)g(x)g(x)иҝҷж ·зҡ„и®Ўз®—й—®йўҳзҡ„еҪўејҸиҖғеҜҹзҪ—зҡ®иҫҫе®ҡеҫӢйҖҡеёёжҳҜд»ҺдёӨиҫ№е…Ҳеҫ—еҲ°еҜ№ж•°пјҢ然еҗҺеҲ©з”ЁзҪ—зҡ®иҫҫе®ҡеҫӢгҖӮ
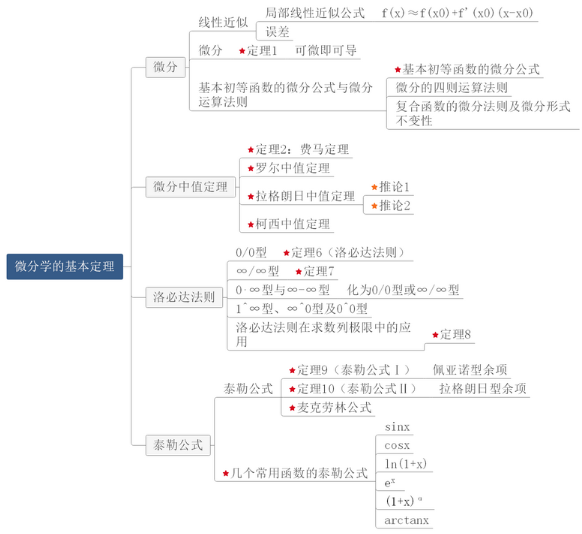
й«ҳж•°жҖқз»ҙеҜјеӣҫ
дә”пјҡеҜјж•°зҡ„еә”з”Ё
еңЁй«ҳдёӯеӯҰд№ еҸҢжӣІжҠӣзү©зәҝзҡ„ж—¶еҖҷпјҢжҲ‘们зҹҘйҒ“жёҗиҝ‘зәҝжҳҜд»Җд№ҲпјҢеңЁиҝҷйғЁеҲҶпјҢжҲ‘们жҠҠжёҗиҝ‘зәҝеҲҶжҲҗж°ҙе№іпјҢеһӮзӣҙпјҢжёҗиҝ‘зәҝпјҢжӣҙз»ҶгҖӮиҰҒзҗҶи§ЈеҒңжӯўзӮ№жҳҜд»Җд№ҲпјҢеҪ“дёҖйҳ¶еҜјж•°еӨ§дәҺ0жҲ–е°ҸдәҺ0ж—¶еҮҪж•°зҡ„еҚ•и°ғжҖ§е’ҢдәҢйҳ¶еҜјж•°еӨ§дәҺ0жҲ–е°ҸдәҺ0ж—¶еҮҪж•°зҡ„еҮ№еҮёгҖӮзЎ®е®ҡжһҒеҖје’ҢжңҖеӨ§еҖјзҡ„ж–№жі•гҖӮ
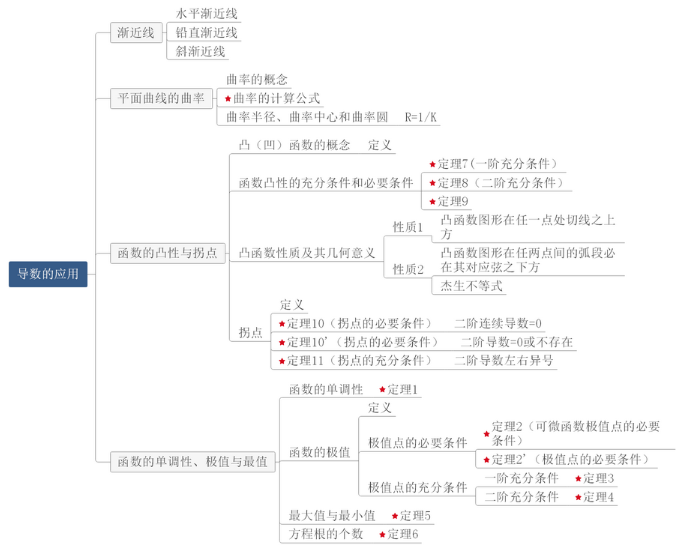
й«ҳж•°жҖқз»ҙеҜјеӣҫ
е…ӯ:з§ҜеҲҶ
з§ҜеҲҶеҲҶдёәеҫ®з§ҜеҲҶе’Ңж•ҙж•°пјҢиҝҷдёӨз§Қж–№жі•зӣёеҗҢпјҢеҸӘжҳҜжұӮж•ҙж•°зӮ№ж—¶д»Јж•°зҡ„иҝҷдёӘйҳ¶ж®өжӣҙеӨҡгҖӮи®°еҝҶдёҺеҺҹеҮҪж•°еҜ№еә”зҡ„еҜјеҮҪж•°зҡ„еҗ„з§Қе…¬ејҸжҳҜи®Ўз®—иҝҷдёӘеҲҶй—®йўҳзҡ„еүҚжҸҗгҖӮ第дәҢпјҢжҖқжғіиҰҒеҸҳеҫ—жҙ»жіјзҒөжҙ»гҖӮзҺ°еңЁпјҢи®©жҲ‘们дёҖиө·иҜҰз»ҶдәҶи§ЈиҝҷйғЁеҲҶеҶ…е®№гҖӮе®һйҷ…дёҠй«ҳзӯүж•°еӯҰ并дёҚйҡҫгҖӮеҸӘиҰҒи®Өзңҹеҗ¬иҜҫпјҢеӨ§еӯҰжңҹжң«иҖғиҜ•е°ұдёҚдјҡжңүй—®йўҳгҖӮеӯҰй«ҳж•°зҡ„ж—¶еҖҷиҰҒеӯҰдјҡжҸҗеүҚйў„д№ гҖӮйӮЈж ·зҡ„иҜқпјҢеңЁиҜҫе ӮдёҠеҫҲе®№жҳ“и·ҹдёҠиҖҒеёҲзҡ„иҝӣеәҰпјҢеҰӮжһңйў„д№ жңүдёҚжҮӮзҡ„й—®йўҳпјҢеҸҜд»ҘеҖјзҸӯеҗ‘иҖҒеёҲжҸҗй—®пјҢз”Ёе…ҡи§ЈеҶігҖӮиҝҷж ·пјҢиҜҫеҗҺз»ғд№ йўҳзҡ„ж—¶еҖҷжӣҙе®№жҳ“гҖӮ
й«ҳж•°жҖқз»ҙеҜјеӣҫ
 еқҡжһңиҠё
еқҡжһңиҠё

